Anscombe quartet - nadaljevanje
4. Da bi odgovorili na prejšnje vprašanje, si je najbolje podatke vizualno ogledati na razsevnem grafikonu.
| Graf med spremenljivkama v prvi skupini | Graf med spremenljivkama v drugi skupini |
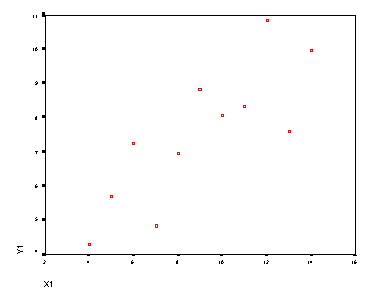 |
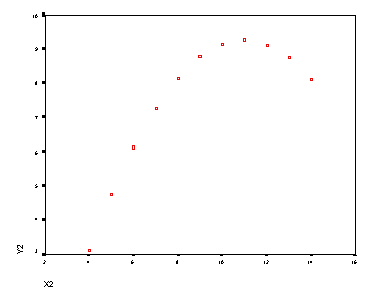 |
| Graf med spremenljivkama v tretji skupini | Graf med spremenljivkama v četrti skupini |
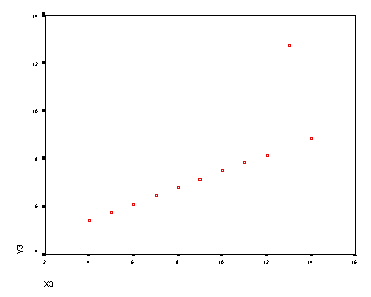 |
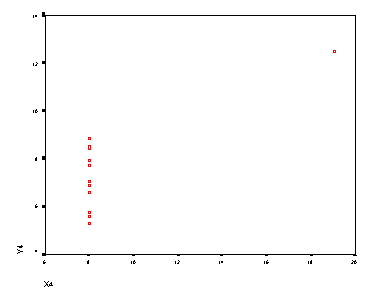 |
5. Očitno gre za štiri popolnoma različne skupine podatkov. Nauk zgodbe: vedno se prepričaj če je zadoščeno predpostavkam linearne regresije!
Podatki
X1 Y1 X2 Y2 X3 Y3 X4 Y4
4,00 4,26 4,00 3,10 4,00 5,39 19,00 12,50
5,00 5,68 5,00 4,74 5,00 5,73 8,00 6,89
6,00 7,24 6,00 6,13 6,00 6,08 8,00 5,25
7,00 4,82 7,00 7,26 7,00 6,42 8,00 7,91
8,00 6,95 8,00 8,14 8,00 6,77 8,00 5,76
9,00 8,81 9,00 8,77 9,00 7,11 8,00 8,84
10,00 8,04 10,00 9,14 10,00 7,46 8,00 6,58
11,00 8,33 11,00 9,26 11,00 7,81 8,00 8,47
12,00 10,84 12,00 9,13 12,00 8,15 8,00 5,56
13,00 7,58 13,00 8,74 13,00 12,74 8,00 7,71
14,00 9,96 14,00 8,10 14,00 8,84 8,00 7,04