On-line slovarček
statističnih pojmov
Matej Kovačič
OSNOVNA STATISTIČNA ANALIZA
Frekvenčna razporeditev
Frekvenčna razporeditev spremenljivke je
porazdelitev vrednosti spremenljivke in njihovih frekvenc. Frekvence ponavadi
zapišemo v obliki relativnih frekvenc oziroma strukturnih odstotkov.
Aritmetična sredina (
)
Aritmetična sredina je poleg mediane,
modusa, geometrijske in harmonične sredine ena izmed najbolj uporabljanih
reprezentančnih vrednosti za spremenljivko. Definirana je kot vsota vseh
vrednosti, deljena s številom enot v populaciji (oziroma v našem primeru v
vzorcu). Primerna je za številske, približno normalno (unimodalno) porazdeljene
spremenljivke.
Analitično
jo izračunamo s pomočjo naslednje formule:
Standardni odklon (SD, s)
Standardni odklon je ena izmed mer
razpršenosti (variabilnosti). Definiran je kot kvadratni koren iz variance, ki
je prav tako ena izmed mer razpršenosti.
Varianco
analitično izračunamo spomočjo naslednje formule:
Aritmetična sredina in standardni odklon
zelo dobro opisujeta približno normalno in unimodalno porazdeljeno
spremenljivko. Vendar pa je unimodalna spremenljivka lahko bolj ali manj asimetrična (v levo ali v desno, odvisno
kam se vleče “rep”) ter bolj ali manj sploščena
(oziroma koničasta). Zato je nujno potrebno izračunati še stopnjo asimertije in
stopnjo sploščenosti. To storimo z naslednjimi dvemi koeficienti.
Koeficient asimetrije (skewness)[1]
Z njim merimo asimetrijo spremenljivke.
Kritične vrednosti:
·
večji od 0 - asimetrija v desno
·
enak 0 - spremenljivka je simetrična (porazdeljuje se
normalno)
·
manjši od 0 - asimetrija v levo
Koeficient sploščenosti (kurtosis)[2]
Z njim merimo stopnjo sploščenosti
spremenljivke. Kritične vrednosti:
·
večji od 0 - koničasta porazdelitev
·
enak 0 - spremenljivka se porazdeljuje normalno
·
manjši od 0 - sploščena porazdelitev
Interval zaupanja (za aritmetično sredino)
Interval zaupanja, ki ga določata njegova
spodnja in njegova zgornja meja, je interval, v katerem se z dano gotovostjo
(ponavadi določimo 95 odstotno) nahaja ocenjevani parameter. Interpretacija je
naslednja: z verjetnostjo tveganja a se
parameter nahaja v tem intervalu.
Analitična
formula za izračun intervala zaupanja za aritmetično sredino je naslednja:
Pri
formuli smo vzeli 95 odstotno gotovost, oziroma 5 odstotno stopnjo tveganja.
T-test
S pomočjo t-testa preverjamo domneve o
enakosti dveh povprečij. To storimo tako, da izberemo neko (neodvisno)
spremenljivko, ki vzorec razdeli na dva dela (dve skupini), nato pa za vsak del
izračunamo povprečje izbrane spremenljivke, povprečji pa med seboj primerjamo.
Hkrati tudi določimo stopnjo značilnosti (a), na
podlagi katere določimo kritično območje.
Analitična
formula za t-test:
|
|
Formula za oceno populacijske variance:
|
Na vzorčnih podatkih izračunamo
eksperimentalno vrednost statistike, in če le-ta pade v kritično območje,
ničelno domnevo zavrnemo in sprejmemo osnovno domnevo ob že prej določeni
stopnji značilnosti a, sicer
pa rečemo, da vzorčni podatki kažejo na statistično neznačilne razlike med
parametrom in vzorčno oceno.
V svoji analizi sem s pomočjo Levenovega testa enakosti varianc
ugotovil ali sta varianci v obeh skupinah enaki (P ³ 0,05) ali ne (P < 0,05) in to tudi upošteval
pri analizi.
Koeficient korelacije med dvema spremenljivkama
Pearsonov koeficient korelacije meri
korelacijsko (stohastično) linearno povezanost med dvema spremenljivkama.
Zavzema lahko vrednosti v intervalu
[-1, 1]. Kritične vrednosti:
·
0: med spremenljivkama ni povezanosti
·
+ 1: pozitivna povezanost (z večanjem vrednosti ene
spremenljivke se veča tudi vrednost druge)
·
- 1: negativna povezanost (z večanjem vrednosti prve
spremenljivke, se manjša vrednost druge)
Pearsonov
koeficient korelacije analitično izračunamo s pomočjo naslednje formule:
pri
čemer je formula za kovarianco 
(ki meri linearno
povezanost med spremenljivkama) naslednja:
RAZVRŠČANJE V SKUPINE
Računanje
evklidske razdalje
Da bi enote
lahko razvrstili v skupine, moramo najprej izmeriti podobnost med posameznima
enotama. Podobnost ugotovimo z mero podobnosti, ki je v bistvu preslikava, ki
vsakemu paru enot (v našem primeru: vsakemu paru študentov iz vzorca) priredi
neko realno število.
Pri razvrščanju
enot, določenih s samimi številskimi spremenljivkami, se najpogosteje uporablja
evklidska razdalja, ki sem jo v svoji nalogi uporabil tudi sam.
Evklidsko razdaljo med enotama X in Y, ki sta opisani z m številskimi spremenljivkami
izračunamo po naslednji formuli:
V svoji nalogi
sem kot opis enot (študentov iz vzorca) vzel 19 odvisnih spremenljivk iz sklopa
“Ambicije za dosego ciljev”.
3.2.
Združevanje v skupine po Wardovi metodi
Wardovo metodo
združevanja v skupine štejemo med hierarhične metode združevanja v skupine, ker
temelji na zaporednem združevanju (zlivanju) dveh ali več skupin v novo
skupino. Mero različnosti med novo skupino, sestavljeno iz skupin 
in 
in neko drugo skupino
v postopku
združevanja v skupine po Wardovi metodi določimo takole:
pri čemer 
predstavlja število
enot v 
, 
pa težišče skupine 
.
3.3 Drevo
združevanja (dendrogram)
Potek
združevanja lahko grafično ponazorimo z drevesom združevanja oz. tim.
dendrogramom. Listi tega drevesa so enote, točke združitve (točke, kjer se ena
veja cepi na več manjših) pa sestavljene skupine. Višina točke ali nivo združevanja (ang. level of fusion) je sorazmerna meri
različnosti med skupinama.
S pomočjo oblike
dendrograma se nato lahko odločimo v koliko skupin bomo razvrstili dane enote.
To storimo tako, da dendrogram na nekem nivoju “odrežemo” (tam, kjer nivoji
združevanja kažejo čimvečjo različnost med skupinami) ter tako dobimo določeno
število odrezanih “vej” drevesa. Število vej nam nato predstavlja število
skupin v katere bomo razvrstili enote.
RAZVRŠČANJE V SKUPINE S POMOČJO METODE GLAVNIH KOMPONENT
Metoda
glavnih komponent
Metoda glavnih
komponent je ena najpogosteje uporabljanih multivariatnih metod. Osnovna
zamisel metode je opisati razpršenost n
enot v m razsežnem prostoru - ki je
določen z m merjenimi spremenljivkami
- z množico nekoreliranih spremenljivk (komponent), ki so linearne kombinacije
originalnih merjenih spremenljivk. Nove spremenljivke - komponente so urejene
od najpomembnejše - to je tiste, ki pojasnjuje kar največ razpršenosti osnovnih
podatkov - do najmanj pomembne - tiste, ki pojasnjuje najmanjši del
razpršenosti opazovanih spremenljivk.
Cilj te metode
je poiskati nekaj prvih komponent, ki pojasnjujejo čim večji del razpršenosti
analiziranih podatkov. Metoda glavnih komponent torej zmanjša razsežnost
podatkov, pri tem pa poizkuša izgubiti čim manj informacij.
Z metodo glavnih
komponent želimo torej poiskati take linearne kombinacije opazovanih spremenljivk,
ki kar se da močno korelirajo z opazovanimi spremenljivkami, oz. pojasnijo kar
se da veliko razpršenosti (variacije) opazovanih spremenljivk. Zato je potrebno
pri metodi glavnih komponent določiti uteži pri linearni kombinaciji
spremenljivk tako, da je varianca te linearne kombinacije največja. Ko
izračunamo prvo komponento z največjo varianco, poiščemo drugo komponento (z
največjo varianco), ki pa s prvo ne sme korelirati. Postopek ponavljamo do
zadnje komponente.
Pomembno je, da
predno računamo glavne komponente spremenljivke standardiziramo.
V naslednjem
koraku moramo ugotoviti koliko komponent je najpomembnejših. V literaturi
obstaja za določanje števila najpomembnejših komponent več pravil:
1.
izbrano število komponent naj
pojasni vsaj 80% skupne variance;
2.
izbrano število komponent naj
pojasni vsaj 50% skupne variance (velja v družboslovju);
3.
lastne vrednosti komponent naj
bodo večje kot povprečna vrednost lastnih vrednosti;
4.
odstotek pojasnjene variance
zadnje še izbrane komponente naj bo vsaj 5 %;
5.
število komponent določimo na
osnovi grafične predstavitve lastnih vrednosti s pomočjo scree diagrama: v koordinatni sistem nanašamo na abscisno os
število komponent, na ordinatno os pa ustrezne lastne vrednosti. Tam kjer se
krivulja na grafu lomi je sugestija za število komponent.
Prikaz
komponent
Nove
spremenljivke - komponente pridobljene s pomočjo metode glavnih komponent sem
potem prikazal v dvorazsežnem razsevnem grafikonu, v katerega sem vključil
kontrolno spremenljivko: SKUP (skupina, dobljena pri razvrščanju v skupine s
pomočjo Wardove metode), uspeh v zadnjem letniku srednje šole (od odličen do
zadosten), vernost (veren/neveren), kraj bivanja (mesto/primestje/vas) in spol
(moški/ženski).
MULTIPLA
REGRESIJA
Konstrukcija Likartove lestvice
Likartovo
lestvico konstruiramo iz večjega števila spremenljivk, ki nam vse merijo isti
koncept. Merjeni koncept želimo zaobjeti v eno samo spremenljivko, ki jo
konstruiramo na naslednji način: vrednosti vseh spremenljivk, ki jih vključimo
v konstrukcijo nove spremenljivke seštejemo ter dobljeno vsoto delimo s
številom spremenljivk. Pri tem pa je seveda potrebno paziti, da so vse
spremenljivke “obrnjene v isto smer”, oz. da vrednosti posamezne spremenljivke
pri vsaki spremenljivki pomenijo oz. na enak način merijo isto. Nova
(konstruirana) spremenljivka je intervalnega tipa.
Multipla regresija
Regresijska
funkcija 
nam kaže, kakšen bi
bil vpliv spremenljivk 
na spremenljivko Y,
če razen teh vplivov ne bi bilo nobenih drugih vplivov. Spremenljivke 
so neodvisne
spremenljivke, spremenljivka Y je odvisna spremenljivka, E pa je člen napake,
ki mu včasih rečemo tudi motnja ali disturbanca. Za i-to enoto seveda velja: 
. Regresijski model pa lahko zapišemo tudi matrično: Y = Xß +
E, pri čimer je:
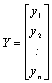
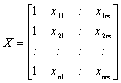
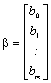
Ko zgradimo regresijski model, seveda nastopi vprašanje,
koliko je regresijski model prilagojen podatkom. Če vemo, da za i-to enoto
velja:
, pri čemer je 
prava vrednost, 
regresijska ocena, 
pa razlika, potem
mora (po metodi najmanjših kvadratov) veljati:
da bo regresijski model čimbolj točen.
Velja torej:
oz. celotna varianca (SST) = pojasnjena varianca (SSR) +
nepojasnjena varianca (SSE).
Vektorsko lahko to zapišemo takole:
Determinacijski koeficient, ali kvadrat multiplega
koeficienta korelacije, ki nam pove odstotek pojasnjene variance analitično
nato izračunamo takole:
Ker je pri determinacijskem koeficientu števec odvisen od
števila neodvisnih spremenljivk, ga je potrebno popraviti:
Celotni regresijski model testiramo z F-testom:
Manjša kot je statistična značilnost F-statistike, boljši
je regresijski model.
FAKTORSKA
ANALIZA
Faktorska analiza
Faktorska analiza je ena izmed metod za
redukcijo podatkov. Pri faktorski analizi gre za študij povezav med
spremenljivkami tako, da poizkušamo najti novo množico spremenljivk, ki predstavljajo
to, kar je skupnega opazovanim spremenljivkam. Množica novih spremenljivk mora
biti seveda manjša od množice merjenih spremenljivk. Z drugimi besedami:
faktorska analiza poizkuša poenostaviti kompleksnost povezav med množico
opazovanih spremenljivk z razkritjem skupnih razsežnosti ali faktorjev, ki omogočajo vpogled v
osnovno strukturo podatkov. Metoda je uporabna v vseh tistih primerih, ko
zaradi različnih vzrokov neposredno merjenje neke spremenljivke ni možno. V tem
primeru merimo samo indikatorje pojma oz. konstrukta, ki ga neposredno ne
moremo meriti. S faktorsko analizo nato ugotovimo ali so zveze med opazovanimi
spremenljivkami (ali indikatorji) pojasnljive z manjšim številom posredno
opazovanih spremenljivk ali faktorjev.
Splošni faktorski model
Osnova faktorskega modela je domneva, da med
spremenljivkami 
(i = 1, ..., m), 
(r = 1, ..., k) in 
(i = 1, ..., m) velja
zveza:
; i = 1, ..., m in k
< m
pri
čemer so 
merjene
spremenljivke, 
skupni faktorji, 
pa specifični faktor,
ki vpliva samo na 
, 
pa je faktorska utež,
ki kaže na vpliv faktorja 
na 
.
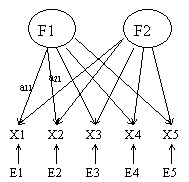
V
matrični obliki splošni faktorski model zapišemo takole:
X = F A’
+ E
Na
osnovi naslednjih predpostavk splošnega faktorskega modela:
·
specifični faktorji so pravokotni med seboj
(cov (
, 
) = 0, če velja i ¹ j)
·
vsak specifični faktor 
je pravokoten na vsak
skupni faktor 
(cov (
,
) = 0, za vsak i in j)
·
skupni faktorji so pravokotni med seboj
(cov (
, 
) = 0, če velja i ¹ j)
·
spremenljivke 
, 
in 
naj bodo centrirane
(E(
) = E(
) = E(
) = 0)
lahko
izpeljemo naslednjo faktorsko enačbo:
S = A A’ + y
Enačbo
lahko zapišemo tudi drugače:
, pri čemer je 
varianca skupnih
faktorjev, 
pa varianca
specifičnih faktorjev (slednja mora biti seveda čim manjša).
S tem smo varianco merjene spremenljivke 
razbili na del, ki je
pojasnjen s kupnimi faktorji in na specifično varianco. Delež variance, ki je
pojasnjena s skupnimi faktorji imenujemo tudi komunaliteta, označujemo
pa jo z 
V prvem delu faktorske analize moramo
najprej izračunati neznane parametre faktorskega modela: faktorske uteži A in
specifične variance y. Pred
tem pa je potrebno preveriti:
·
identifikabilnost
faktorskega modela (ugotoviti moramo, ali faktorske uteži A in
specifične faktorje y sploh lahko
ocenimo)
Potreben (ne pa tudi zadosten) pogoj za
identifikacijo faktorskega modela je:
, pri čemer je m
število spremenljivk vključenih v faktorski model, k pa število faktorjev.
Če ta pogoj ni izpolnjen, je model prefaktoriziran, kar pomeni, da imamo
faktorje, ki že opisujejo merske napake. Sum na prefaktorizacijo nastopi
takrat, ko npr. korelacijski koeficienti padejo iz intervala [-1, 1] ali ko se
pojavi negativna varianca.
·
enoličnost
ocen parametrov (ali lahko te parametre ocenimo enolično - z eno
samo oceno)
Pri enoličnosti pa nastopi problem da se
parametra A sploh ne da enolično izračunati. Zato računamo v dveh korakih:
najprej izračunamo y
(zakoličimo skupni prostor - ocenimo komunalitete), nato pa na podlagi tega
izračunamo A. Postopek ponovimo večkrat, dokler model ne skonvergira.
Pri tem delu faktorske analize lahko
uporabimo več različnih metod. Kratek opis štirih najbolj pogostih, ki sem jih
tudi uporabil v svoji nalogi podajam v spodnji tabeli:
|
ime
metode |
osnovni
princip |
ocena
komunalitete |
|
metoda
glavnih osi |
maksimizira
varianco skupnih faktorjev |
več
načinov, kvadrat koeficienta multiple korelacije |
|
image |
vsako
spremenljivko regresira z ostalimi |
iterativno |
|
metoda
najmanjšega verjetja |
poišče
najboljšo oceno za reprodukcijo variančno kovariančne-matrike S |
iterativno |
|
alfa |
maksimizira
generabilnost faktorjev |
iterativno |
Rotacije
Drugi korak faktorske analize je rotacija. S
pomočjo rotacije prečistimo strukturo. Bistvo rotiranja namreč je, da dobimo
teoretično pomembne faktorje in čim enostavnejšo faktorsko strukturo. Če namreč
dobljene rešitve ne moremo dobro interpretirati, lahko dobljeno rešitev v
skupnem prostoru, ki je določen s skupnimi faktorji transformiramo tako, da jo
zarotiramo. Matematično to pomeni, da matriko A pomnožimo z transformacijsko
matriko M (A* = A M). Rešitev A* enako dobro reproducira
originalne podatke kot prvotna rešitev A.
Za rotacijo se odločamo predvsem takrat, ko
skupnih faktorjev ne moremo smiselno interpretirati - če so npr. projekcije
iste spremenljivke precejšnje na več faktorjih, ali pa če imamo splošen faktor (projekcije vseh
spremenljivk na prvi faktor so precejšnje). Ločimo dve vrsti rotacij:
·
pravokotne, kjer
so rotirani faktorji neodvisni med seboj (znana metoda je npr. varimax, ki maksimizira varianco
kvadratov uteži v vsakem faktorju in s tem poenostavlja strukturo po stolpcih);
·
poševne, kjer
so rotirani faktorji odvisni med seboj, med njimi ni pravega kota in faktorji
med seboj korelirajo (pri tem sem uporabil metodo oblimin). V primeru poševnih rotacij lahko spremenljivke (točke v
poševnem koordinatnem sistemu) projiciramo na poševne faktorje na dva načina:
·
vzporedno, pri čemer dobimo pattern uteži, ki so parcialni koeficienti korelacije med
spremenljivko in faktorjem in. predstavljajo “suhi vpliv” spremenljivke na
faktor;
·
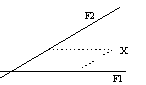
pravokotno, s čemer dobimo strukturne uteži, ki so navadni koeficienti korelacije med
spremenljivko in faktorjem.
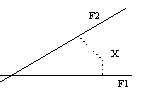
V
primeru pravokotnih faktorjev so pattern
in strukturne uteži seveda enake.
Vsebinsko so poševne rotacije boljše, v
praksi pa nastopijo problemi s kriterijsko funkcijo. Zato ponavadi najprej
naredimo poševno rotacijo, nato pa pogledamo kakšne so korelacije med faktorji.
Če so korelacije med faktorji majhne (manj od 0,20), naredimo pravokotno
rotacijo, sicer pa ne, saj bi bila v slednjem primeru struktura preveč
vsiljena.
Določitev
faktorskih vrednosti na enotah
V tretji, zadnji fazi faktorske analize
določimo še faktorske uteži na posameznih enotah. Eden izmed načinov za
določitev teh uteži je regresijska ocena faktorske vrednosti. Pri tem dobimo
ocenjeno faktorsko vrednost 
in ne prave faktorske
vrednosti F. Korelacije med 
zato ne bodo take kot
med F, lahko pa se spremeni tudi smer faktorja 
.
DISKRIMINANTNA ANALIZA
Diskriminantna
analiza
Osnovni cilj
diskriminantne analize je poiskati tako linearno kombinacijo merjenih
spremenljivk, da bodo vnaprej določene skupine med seboj čimbolj različne,
napaka pri uvrščanju enot v skupine pa bo čim manjša. Pri diskriminantni
analizi tako iščemo tiste razsežnosti podatkov, ki kar najbolj pojasnjujejo
razlike med skupinami. Iščemo torej dimenzijo, kjer so skupine čimbolj ločene.
Diskriminantna analiza ima zato funkcijo pojasnjevanja, pa tudi napovedovanja,
saj je eden izmed ciljev diskriminantne analize tudi ta, da (nove) enote kar se
da dobro prirejajo vnaprej danim skupinam.
Predpostavke
diskriminantne analize
Da je diskriminantna naliza sploh možna, mora biti
zadoščeno naslednjim pogojem:
·
število skupin k mora
biti večje ali vsaj enako 2
·
v vsaki skupini morata biti
vsaj dve enoti (zaradi variabilnosti v skupini)
·
število spremenljivk p
mora biti manjše od n - 2, pri čemer je n število enot v vzorcu
·
spremenljivke morajo biti vsaj
intervalnega tipa, lahko pa uporabimo tudi dobre ordinalne spremenljivke
·
nobena spremenljivka ne sme
biti linearna kombinacija preostalih spremenljivk (prepoved multikolinearnosti)
·
variančno-kovariančna matrika
mora biti za vsako skupino enot (približno) enaka (“variance” pri vseh skupinah
morajo biti približno enake)
·
pri statističnem ocejevanju se
predpostavlja, da so v vsaki skupini enot spremenljivke dobljene iz populacije
z večrazsežno normalno porzdelitvijo spremenljivk
Diskriminantna analiza na dveh ali več skupinah
Diskriminantna
spremenljivka Y v primeru dveh skupin, ki je linearna kombinacija merjenih
spremenljivk
: 
, je definirana tako, da je kvocient razlik povprečij
diskriminantne spremenljivke v obeh skupinah 
in 
glede na varianco
diskriminantne spremenljivke v skupini maksimalen. V primeru večih skupin razlike
med skupinami lahko popišemo z več diskriminantnimi spremenljivkami - največ
jih je lahko največ min (p, k-1) [p je število spremenljivk, k pa število skupin].
Postopek za izračun diskriminantnih spremenljivk je v tem
primeru naslednji:
·
označimo vsoto kvadratov in
produktov odklonov od skupnega povprečja 
:
·
isto naredimo še za vsako
posamezno skupino:
; variabilnost znotraj skupin je enaka 
·
izračunamo še vsoto kvadratov in
produktov odklonov med skupinami:
B = T - W
V primeru večih skupin je tako diskriminantni kriterij
naslednji:
oziroma: 
; 
je ocena uteži
Kriteriji
selekcije med spremenljivkami v diskriminantni analizi so Wilksova lambda,
Mahalanobisova razdalja in F-test. Za preverjanje domneve o številu statistično
značilnih diskriminantnih spremenljivkah pa se uporablja Bartletov test.
Pravila uvrščanja enot v skupine
Ko imamo
izračunano diskriminantno spremenljivko 
, k-to enoto uvrstimo v tisto skupino 
, za katero velja, da je razlika med 
najmanjša. Povedano
drugače: enoto uvrstimo v tisto skupino, ki ima povprečje diskriminantne
spremenljivke čim bolj podobno vrednosti diskriminantne spremenljivke te enote.
Klasifikacijska tabela
Glede na
izračunano diskriminantno spremenljivko vsako enoto ponovno uvrstimo v svojo
skupino, pri tem pa dobimo odstotek pravilno uvrščenih enot. Diskriminantne spremenljivke
najbolje razvrščajo enote, če je odstotek pravilno razvrščenih enot 100 %.
Spodnja meja kvalitete razvrščanja pa je odstotek enot, ki bi bile pravilno
uvrščene ob naključnem razvrščanju. V primeru dveh skupin je tako spodnja meja
50 % enot, v primeru treh pa 33,3 %.
LISREL MODEL
Model in
modeliranje
Model je
miselna, formalna ali materialna konstrukcija, ki glede na cilje proučevanja
ustrezno nadomešča dejanski pojav, ki ga proučujemo. Z modelom povzamemo
bistvene značilnosti proučevanega dejanskega pojava in s tem poenostavimo oz.
včasih celo sploh omogočimo njegovo proučevanje. Funkcija modela je predvsem
pojasnjevanje, pa tudi upravljanje in napovedovanje pojava. Model in dejanski
pojav nista istovetna, saj model le ralativno ustreza dejanskosti.
Modeliranje pa
je ena izmed splošnih znanstvenih metod raziskovanja. Razpeto je med dvema
dilemama: ustreznost dejanskemu stanju ter obvladljivost modela.
Osnovni
elementi vzročnih teorij, formulacija vzročnih teorij ter vzročni modeli
Med dvema
spremenljivkama lahko velja povezanost (kovariiranje) ali odvisnost
(vzročnost). Ločimo naslednje tipe povezanosti:
·
navidezna povezanost: povezanost med spremenljivkama X in Y nastane zaradi
skupne vzročne spremenljivke Z.
·
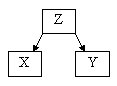
direktna in indirektna (posredna) vzročna povezanost: spremenljivka X vpliva na spremenljivko Z preko
spremenljivke Y, ki jo imenujemo tudi intervenirajoča spremenljivka.
ali tudi: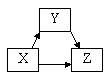 
·
recipročna vzročna povezanost: spremenljivki vzročno vplivata druga na drugo, vsaka z
drugačnim vzročnim učinkom
·
pogojna povezanost: na povezavo med dvema spremenljivkama vpliva tretja
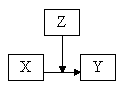
Prvi korak
formulacije vzročnih teorij je da raziskovalec na osnovi razpoložljivega
materiala (dokumentov, študij, raziskav) opredeli:
·
relevantne spremenljivke,
·
vzročno zaporedje
spremenljivk,
·
vzročne domneve,
nato pa na
osnovi teoretičnega poznavanja problema skuša preveriti vzročne domneve. Problem pa je v tem, da obstoja
vzročnosti ni mogoče dokazati. Iz podatkov namreč lahko določimo le
stopnjo kovariiranja (povezanosti), vendar pa kovariiranje ni dokaz za vzročno
povezanost, saj je lahko le rezultat skupnega vzroka obeh obravnavanih spremenljivk.
Torej lahko preverjamo le, če je vzročna domneva napačno postavljena. Še več!
Za isto teorijo lahko postavimo različne modele, in lahko se zgodi da nobenega
ne zavrnemo. Resničnost torej lahko pojasnimo z različnimi teorijami oz.
različnimi modeli.
Če povezanost in navidezna povezanost nista enaki je
možno naslednje:
1. vzročni vpliv obstaja
2. izpuščen je pomemben skupni vzrok
Zato je v model
potrebno vključiti vse relevantne skupne vzroke. Ker pa bi s tem lahko dobili
neskončen proces dodajanja spremenljivk, se lahko odločimo da za nekaj
spremenljivk, ki jih v teoriji potrebujemo predvsem kot pojasnjevalno moč, ne
iščemo skupnih vzrokov (jih ne pojasnjujemo). Te spremenljivke imenujemo
eksogene (označujemo jih z X), ostale, ki jih pojasnjujemo pa endogene
(označujemo jih z Y). Tako lahko vzročne teorije poenostavimo s tem, da
izpustimo intervenirajoče spremenljivke, ali pa tiste spremenljivke, ki
vplivajo ali na vzročne ali na posledične spremenljivke, vendar ne na obe
hkrati. Nikakor pa ne smemo izpustiti spremenljivk, ki nam pojasnjujejo skupne
vzroke. Seveda pa se moramo zavedati da model s tem, ko ga poenostavljamo,
hkrati tudi siromašimo.
Motnje oz.
disturbance v vzročnih modelih
Motnje v
vzročnih modelih označujemo s simbolom x, vzroki zanje pa so:
·
šibka formulacija teorij
(manjkajo pomembne spremenljivke)
·
prekompleksnost teorij
(zavestno izpuščamo manj pomembne spremenljivke)
·
nenapovedljivost, slučajnost
(napake respondentov)
·
nezanesljivost merjenja (slabi
indikatorji)
Modeli
linearnih strukturnih enačb
Najprej definirajmo naslednja dva pojma:
·
linearnost: nastopi ko vrednost vzročne spremenljivke ne
vpliva na velikost vzročnega učinka;
·
aditivnost: vzročna
učinka sta aditivna, če na velikost posameznega vzročnega učinka ne vpliva
vrednost druge vzročne spremenljivke.
Če imamo vzročne
učinke, za katere lahko predpostavimo linearnost in aditivnost, lahko za vsako
endogeno spremenljivko Yi napišemo linearno enačbo:
[če so spremenljivke
standardizirane a ne potrebujemo]
pri čemer je pomen oznak naslednji:
p - število endogenih spremenljivk
q - število eksogenih spremenljivk
- motnja za i-to
endogeno spremenljivko
- vzročni učinek j-te
endogene spremenljivke na i-to endogeno spremenljivko
- vzročni učinek j-te
eksogene spremenljivke na i-to endogeno spremenljivko
- povezanosti med
eksogenimi spremenljivkami (korelacija)
- povezanosti med
motnjami (varianca motnje)
V modelu linearnih strukturnih enačb predpostavimo:
·
da je povprečje motenj enako
nič: 
;
·
da so
motnje in eksogene spremenljivke pravokotne oz. nepovezane med seboj: cov(
Xj) = 0;
·
motnje med seboj niso povezane
;
·
povezanosti med
spremenljivkami X so različne od 0: 
¹ 0.
Dobro je tudi,
da spremenljivke standardiziramo, saj se s tem izognemo zmedi v interpretaciji,
ki nastane zaradi vpliva merske lestvice na velikost parametrov učinka.
Zveze med
kovariancami ali korelacijami in strukturnimi parametri
Pomemben korak
analize je tudi vzpostavitev zveze med informacijami, ki jih lahko izračunamo
iz podatkov ter strukturnimi parametri, ki so osnovna značilnost vzročnih
teorij (
,
,
,
). Te zveze je mogoče dobiti z dekompozicijskimi pravili:
I. dekompozicijsko pravilo:
Korelacijski
koeficient (empirično izmerjena korelacija) med dvema spremenljivkama je enak vsoti direktnih učinkov, indirektnih
učinkov, navideznih povezav ter skupnih učinkov.
Vsak indirektni
učinek, navidezna povezanost in skupni učinek je lahko izražen kot produkt parametrov, ki povezujejo dve
spremenljivki.
II. dekompozicijsko pravilo:
Celotna varinca
endogene spremenljivke Y je enaka količini variance pojasnjene z vzročnimi
spremenljivkami te endogene spremenljivke in količine nepojasnjene variance.
Za vsako
endogeno spremenljivko lahko dobimo delež pojasnjene variance z vsoto produktov direktnih učinkov in
korelacijskih koeficientov te
endogene spremenljivke in vsake od
njenih vzročnih spremenljivk.
Potrebni
pogoj za identifikacijo vzročnega modela
Razliko med
številom enačb in številom strukturnih parametrov imenujemo število prostostnih stopenj. Potrebni
pogoj za identifikacijo modelov strukturnih enačb je, da je število prostostnih
stopenj enako ali večje od nič.
Iz tega sledi
zaključek, da so modeli z eno strukturno enačbo (regresijski modeli) vedno
identifikabilni.
Lisrel
model
Vzročni model
lahko v splošnem (matrično) zapišemo takole:
in sicer z
naslednjimi predpostavkami:
·
(I-B) je nesingularna matrika
·
E(x) = 0
·
je nekoreliran z X.
Oceniti je torej potrebno naslednje parametre:
B, G in y = cov(x)
potrebni pogoj za identifikacijo modela pa je
kjer je p
število endogenih spremenljivk, q
število eksogenih spremenljivk, t pa
število neznanih parametrov v modelu.
Lisrel model pa je določen s tremi (matričnimi) enačbami:
·
strukturni model:
·
merski model za Y:
·
merski model za X:
z naslednjimi predpostavkami:
1.
z ne korelira z x
2.
e ne korelira z h
3.
d ne korelira z x
4.
z, e ter d med seboj ne korelirajo
5.
matrika I - B je nesingularna
(če je singularna dobimo nesmiselne rezultate)
Ocenjevanje
modela
Naš teoretično
postavljen model lahko ocenimo z naslednjimi metodami:
·
metoda najmanjših kvadratov
(ULS)
·
metoda posplošenih najmanjših
kvadratov (GLS)
·
metoda največjega verjetja
(ML)
Vsaka metoda
izračuna funkcijo prileganja F. Le-ta je vedno nenegativna. Če gre za popolno
prileganje je anaka 0. Funkcijo F program Lisrel minimizira iterativno. Metoda
ML predpostavlja večrazsežno normalno porazdelitev merjenih spremenljivk,
dokazano pa je, da sta metodi ML in GLS precej robustni na nenormalnost.
Cenilke se približno normalno porazdeljujejo ob predpostavki, da so za velike
vzorce (400 enot ali več) izračunane standardne napake ocen parametrov.
Statistično
značilnost posameznega parametra izračunamo tako, da izračunamo 95-odstotni
interval zaupanja, za ta parameter.
Če je celoten
interval pozitiven, oz. negativen, lahko s 5-odstotnim tveganjem sprejmemo
domnevo o vzročnem učinku, če pa je interval delno pozitiven, delno pa
negativen, pa rečemo, da vzročnega učinka ni.
Program Lisrel
omogoča test modela v celoti (kako se prilega podatkom), vendar je poleg teh
statistik potrebno pogledati tudi smiselnost dobljene rešitve:
·
ali so vse ocene parametrov v
znanih intervalih (da ne presežejo svojega definicijskega območja)
·
ali so standardne napake
dovolj majhne
·
kolikšen je odstotek
pojasnjene variance endogenih spremenljivk (
za standardizirane podatke)
Poleg tega
Lisrel lahko izračuna še 
mero celotnega
prileganja podatkom. Izračunati jo je možno, če je število prostostnih stopenj
df večje od nič:
Pri
tem velja: večja kot je statistična značilnost (in manjši kot je 
), bolj se model prilagaja podatkom.
ZANESLJIVOST MERJENJA
Kvaliteta merjenja
Ob merjenju
spremljamo predvsem dve razsežnosti kvalitete merjenja:
·
zanesljivost merjenja (obravnava slučajne napake),
·
veljavnost merjenja (obravnava sistematične napake).
Zanesljivost je potreben, ne pa tudi zadosten pogoj za
dober merski postopek.
V postopku
merjenja nastopajo moteči dejavniki, ki vplivajo na rezultat merjenja. Rezultat
njihovega delovanja so merske napake. Merska napaka je razlika med dejansko in
izmerjeno vrednostjo. Ločimo dve vrsti merskih napak:
·
slučajne napake, ki povečujejo varianco izmerjenih vrednosti, na ocene
pravih vrednosti pa ne vplivajo;
·
sistematične napake, ki povzročajo pristranske ocene pravih vrednosti.
Zaradi zgornjih ugotovitev velja formula:
izmerjena vrednost = dejanska
vrednost + slučajne napake + sistematične napake
Grafično pa bi zanesljivost in veljavnost merjenja lahko
prikazali takole:
|
(ne)zanesljivost merjenja |
(ne)veljavnost merjenja |
Legenda:
|
Klasična testna
teorija se ukvarja samo z
zanesljivostjo merjenja, saj predpostavlja da je merjenje veljavno. Ob tej
predpostavki pa velja formula:
izmerjena vrednost = dejanska vrednost + slučajne napake
kar lahko zapišemo tudi takole: 
(velja za i-to meritev). Matrično enačba
izgleda takole:
X = T + E
Ob pogoju, da
ostaja prava vrednost konstantna, in da se postopek merjenja ne spreminja
velja, da dejanska vrednost verjetnostna limita, ki se ji izmerjena vrednost
približuje, če število ponovljenih meritev narašča čez vse meje.
Predpostavke
klasične testne teorije so, da je aritmetična srenida napak enaka nič, da so
dejanske vrednosti in napake pri eni alimed različnimi meritvami med seboj
neodvisne ter da so slučajne napake med seboj neodvisne.
Metode ocenjevanja zanesljivosti
Cilj merjenja je
čimbolj natančna ocena dejanskih vrednosti. Ker postopki merjenja niso
popolnoma zanesljivi, enkratna merjenja ne dajo dovolj dobrih ocen dejanskih
vrednosti. Glede na to, da je dejanska vrednost verjetnostna limita, ki se ji
izmerjena vrednost približuje, če število ponovljenih meritev narašča čez vse
meje, lahko rečemo, da je zanesljivost funkcija števila neodvisnih meritev.
Zvezo med vsoto n paralelnih meritev 
ter zanesljivostjo posamezne meritve (ob
predpostavki, da je zanesljivost posamezne meritve znana) lahko opišemo z
Spearman-Brownovo formulo:
|
|
; pri čemer je n število meritev, |
zanesljivost
posamezne meritve, 
pa
zanesljivost vsote vseh meritevVelja še:
; iz česar sledi da več kot je ponovitev, bolj je merjenje
zanesljivo, oz. hitrejre pridemo do dobre (zanesljive) informacije.
Za ocenjevanje zanesljivosti merjenja ločimo dve vrsti
metod:
·
metode stabilnosti,
·
metode interne
konsistentnosti.
Metode stabilnosti
Osnovna ideja
teh metod je, da na istih enotah po določenem času ponovimo merjenje.
Zanesljivost merjenja spremenljivke X je korelacijski koeficient med
paralelnima meritvama te spremenljivke. Če je ta koeficient enak 1, gre za
popolno stabilnost. Poznamo:
·
Test-retest (korelacijski koeficient med dvema ponovljenima
merjenjema iste (paralelno merjenje) spremenljivke). Isto vprašanje postavimo v
dveh časovnih točkah. Problem je spominjanje prejšnjega odgovora ter sprememba
vrednosti spremenljivke v času.
·
Metoda alternativne oblike (korelacijski koeficient med merjeno spremenljivko in
drugo enakovredno spremenljivko). Tudi v tem primeru tako kot prej ponovimo
postopek merjenja na istih enotah, vendar ne uporabimo enakega, pač pa
različno, a enakovredno obliko merjenja (alternativna vprašanja, lestvice).
Problem spominjanja je tukaj manj izrazit, problem nastopi pri vprašanju, ali z
obema vprašanjema sploh merimo isto latentno spremenljivko.
Metode interne konsistentnosti
Te metode
temeljijo na merjenju istega konstrukta z več enakovrednimi spremenljivkami
(različnimi indikatorji, ki merijo isti koncept) v istem času. Poznamo:
·
Metoda razpolovitve
(split-half method). Opazovane spremenljivke
razvrstimo v dve skupini, jih v vsaki skupini seštejemo ter izračunamo
korelacijski koeficient med skupinama. Zanesjlivost dobimo s pomočjo naslednje
formule: 
. Če imamo 2n opazovanih spremenljivk, je
možnih kombinacij razvrstitev v dve skupini natanko 
.
Problem te metode je torej v tem, da je možnih kombinacij kako spremenljivke
razvrstiti v dve skupini veliko, različne možne kombinacije pa dajo različne
ocene zanesljivosti.
·
Chronbachov a. Le-ta temelji na variancah in kovariancah med merjenimi
spremenljivkami, ki merijo isti konstrukt. a je definirana na intervalu [0, 1]. Če je vrednost a večja od 0,80, pravimo, da je merski postopek zanesljiv.
Chronbach je dokazal, da je a enak povprečju vseh možnih
razpolovitev.
·
Metoda glavnih komponent in Q. V primeru, da opazovane spremenljivke res merijo le eno
latentno spremenljivko, bo lastna vrednost prve komponente velika (prva
komponenta bo pojasnila večino variance merjenih spremenljivk), ostale lastne
vrednosti pa bodo nizke. Vrednost Q, ki tudi meri zanesljivost
merjenja izračunamo takole:
|
|
; pri čemer je n število spremenljivk (oz. indikatorjev
latentne spremenljivke), |
Vpliv (ne)zanesljivosti merjenja na ocene statističnih
parametrov
1.
Aritmetična
sredina opazovane vrednosti je enaka aritmetični sredini dejanske
vrednosti.
2.
Varianca
opazovane vrednosti je večja od variance dejanske vrednosti.
3.
Kovarianca
med dvema dejanskima spremenljivkama je neodvisna od zanesljivosti
merjenja obeh spremenljivk.
4.
Korelacijski
in regresijski koeficienti opazovanih vrednosti so manjši od koeficientov
dejanske vrednosti.
V družboslovni metodologiji in raziskavah so
mejne vrednosti ki določajo dobro korelacijo in visok odstotek pojasnjene
variance precej nižje kot v npr. medicini ali tehniki. Ker je vedenje ljudi
manj stabilno kot npr. vedenje nekega tehničnega ali fiziološkega sistema
(rekli bi lahko da smo ljudje bolj kompleksni sistemi), je zato tudi merjenje
vedenja (stališč,...) ljudi bolj nezanesljivo. Ta nezanesljivost pa se odraža v
slabih ocenah parametrov, zato so kriteriji za ocenjevanje moči korelacijskih
in regresijskih koeficientov v družboslovju nižji kot drugod.