FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Ampere's Law |
 
|
Return to the Advanced Level Page.
Ampere's Law is a useful relation that is analogous to Gauss's Law. It is the relation between the tangential component of magnetic field at points on a closed path and the net current through the area bounded by the path. It is formulated in terms of the line integral of B around a closed path:
(Equation 6-72)
We are going to divide the path into really tiny segments dl and for each one calculate the scalar product of B and dl. Generally B varies, but the B at the location of the dl is going to be used so it won't be a problem. The circle on the integral sign means it'll be computed on a closed path, where the start and the end are the same point. It is analogous to the Gaussian surface--you do not really need a physical object there.
The simplest conductor we can consider is a long straight one with current I, passing through the center of a circle of radius r in a plane perpendicular to the wire. The field has a magnitude of m0I/2pr at every point in the circle. We derived that earlier, and it is tangent to the circle at each point. So for every point on the circle B|| = B = m0I/2pr. The line integral of B around the circle is:
(Equation 6-73)
In other words, the line integral of B is equal to m0 multiplied by the current passing through the area bounded by the circle.
So basically, Ampere's Law says:
- The line integral of the magnetic field B around any closed path is equal to m0 times the net current across the area bounded by the path.
- If B is everywhere tangent to the integration path and has the same magnitude at every point on the path, then its line integral is equal to B times the circumference of the path.
- If B is everywhere perpendicular for part of the path, for that portion of the path makes no contribution to the line integral.
- In the integral, B is always the total magnetic field at each point on the path. The field is caused partly by currents linked by the path and by currents outside. Even when no current is linked to the path, the field at points on the path might not be zero, but there the integral is zero.
- When you choose an integration path, two principles that might help are that the points at which the field is to be determined must lie on the path and that the path must have enough symmetry so that the integral can be evaluated.
Magnetic Field of a Solenoid
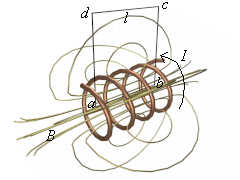Now we are going to put our newly found knowledge to use.
We are going to play with a solenoid carrying a current I.
A segment of that solenoid is displayed on the illustration at right (click on the illustration for a VRML model of the solenoid).
The resultant field at any point is the vector sum, as it always is, of all the coils in the wire.
If the solenoid is very large compared to its cross-sectional diameter, the internal field near its center is very nearly uniform and parallel to the axis.
The external field near the center is very small.
We can use Ampere's law to find the internal field.
Our path is going to be a very nice rectangle, abcd.
cd is going to be so far away that the field contribution is negligible.
bc and ad are parallel to the field so the field there is zero.
The only side of the path that makes any contribution is ab.So if n is the number of turns per unit length of the windings, then the number of turns in length l is nl. Each of these turns passes once through the rectangle abcd and carries a current I. The total current through the path is nlI and using Ampere's Law:
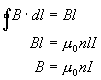
(Equation 6-74)
Magnetic Field of a Toroid
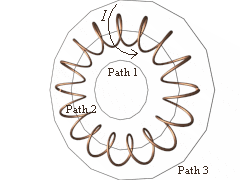The illustration at right is a toroid, a solenoid that is looped back on itself (click on the illustration for a VRML model of the toroid).
It is wound with a wire carrying current I
The three circles around the toroid are the paths used in our analysis using Ampere's law.- Path 1: By symmetry, if there's a field there, it will be tangent to the path. Each turn of the winding pass twice through the area in the path, carrying equal currents in opposite directions, which means, you guessed it, a net current of zero. If I = 0, then B = 0 and there is no field.
- Path 3: Here as well, if there was a field it would be tangent as well. So, Ampere's law says the field B must be zero by the same reasoning as the previous one. What this means is that the field of a toroidal solenoid is confined wholly in the space of the windings.
-
Path 2: Now in this path, a circle of radius r, the B field is tangent to the path, and:
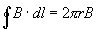
(Equation 6-75)
Each turn of the winding only passes once through path 2 and the total current is NI, N being the total number of turns in the toroid. Then:
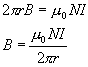
(Equation 6-76)
The B field is not uniform over a cross section of the core because the path length l is larger at the outer side of the section. But if the radial thickness of the core is small compared to toroid radius r, the field only varies a little. Thus, considering that 2pr is the circumference of the toroid and that n/2pr is the number of turns per unit length n, the field may be written as B = m0nI.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar