FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Electric Fields |
 
|
Return to the Advanced Level Page.
In this section, we will be working with electric fields and what they look like with different shaped conductors. To review, here are a few rules about electric field lines:
- No field lines originate or terminate in the space surrounding a charge. It has to start at a positive charge and end at a negative charge.
- Field lines never cross. At any one point, the resultant field (and the field lines that represent it) can have only one direction.
- Since the field exists at all points, you could technically fill all of space with field lines. But you can represent it with only a number of field lines that can be used to indicate the magnitude of the field and its direction. The closer the lines, the denser and stronger the field.
(Equation 6-1)
And the electric field at charge q' is:
(Equation 6-2)
Now that we reviewed these concepts, we can begin deriving. The next three derivations will give you some experience with the various types of concepts and integrals that we will be dealing with later.
Ring-Shaped Conductor
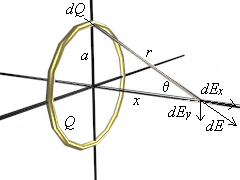The conductor is a ring of radius a, and carries a total charge of Q.
Now we are going to find the electric field at a point x from the center along a line perpendicular to the ring.
You can see the illustration at right to visualize this setup (click on the illustration for a VRML model of the ring).First you need to break down the ring into sections of size ds because you will need to integrate along the ring. The charge of the segment ds is dQ, a small part of the total charge. At point we are looking at, the element of charge causes an electric field contribution dE having a magnitude of:
(Equation 6-3)
Now just look at the figure. If we were to break down the components of the electric field contribution of dQ into x and y components, what do you think would happen to the y components of the field? It turns out that they will cancel out with the y components on the opposite side of the ring. This means that we only need to consider the components of dEx of this field, and it is defined as follows:
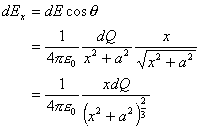
(Equation 6-4)
So to find the total of all the x components, simply integrate:
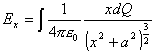
(Equation 6-5)
On the right side everything except dQ is a constant so they can be moved outside the integral. Then integrate to get:
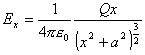
(Equation 6-6)
That is your answer folks.
Long Charged Wire
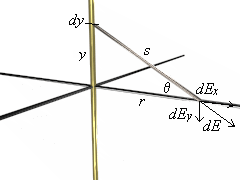Now you have a long charged wire of length 2L that lies along the y-axis and has a charge per unit length of l.
We will find the electric field caused by this wire at point P, a distance r from the midpoint of the wire.
You can see the illustration at right to visualize this setup (click on the illustration for a VRML model of the wire).Now, just like before, divide the wire into infinitesimal segments dy, and the charge of which is known to be dq, where dq = l dy. The distance s from any segment at position y to point P is:
(Equation 6-7)
Thus, the contribution dE to the field at P due to this piece is given as:
(Equation 6-8)
To find the total field at P we need to sum the contributions of all the segments, which means we need to integrate. However, we need to break it all down to components first. Again, because of the symmetry, the y components are going to cancel out, and we only need to worry about the x components:
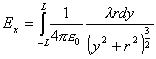
(Equation 6-9)
The integraton can be done by trigonometric substitution or by a table of integrals. Since this isn't calculus I trust that you will go look on your own. Once you integrate it you get:
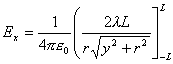
(Equation 6-10)
Now, if the length of 2L is much longer than the distance r (if the wire is basically infinitely long), then r becomes negligible compared to L inside that square root. So effectively it simplifies down to:
(Equation 6-11)
Jackpot! You are done with this incessantly long thin wire.
Infinite Plane Sheet of Charge
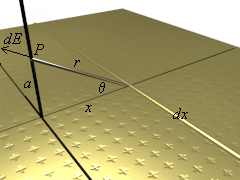This is the last one, we promise.
A positive charge is distributed uniformly over an entire xy-plane, with a surface density of charge s.
We will find the electric field at point P, a distance a from the plane.
You can see the illustration at right to visualize this setup (click on the illustration for a VRML model of the sheet).Now here is where we "cheat" a little. Divide the sheet into long strips of width dx, parallel to the y-axis. Now do you notice how they resemble the long charged wire? We can use that to help us along.
But first the area of a portion of the strip of length L is Ldx, and the charge dq on the strip is:
So the charge per unit length is:
(Equation 6-12)
With the equation from the long wire we now setup dE in the xz-plane now:
(Equation 6-13)
Now again we use symmetry and we notice that all the contributions in the x direction cancel each other out and only the upward field in the z-direction matters. So the resultant electric field at P is in the z-direction and can be defined as:
Since there are dE's on both sides, naturally we think to integrate and we get the following:
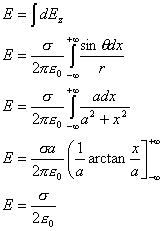
(Equation 6-14)
Before you start going crazy wondering where a actually went, it was the distance between the point and the plane and one would imagine that value would be pretty important, but what it tells you is that the intensity of the field created by the sheet is independent of the distance from the charge. More simply, the field is uniform and normal to the plane and does not weaken when you get away from the sheet.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar