FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Gauss's Law |
 
|
Return to the Advanced Level Page.
Kal Friedrich Guass (1777-1855) was a German scientist and mathematician known for a relation known as Gauss's Law. His law was a statement of an important property of electrostatic fields. With your understanding of field lines, it will be easy for you to understand Gauss's Law.
The field of an isolated electric charge q can be represented by field lines that radiate outward, right? Let's say we surround this charge with a sphere of radius R with the charge being at the center. This sphere's surface is, therefore 4pR2. So if the number of field lines from the charge q is N, then the number of lines per unit surface area on the sphere is N/(4pR2).
Now what if we surround this sphere with another one, with a radius of 2R? The surface area is now 16pR2 and the number of lines per unit area is only N/(16pR2). The line density is only a fourth of the first sphere, which makes sense since the radius of the second sphere is twice that of the first.
However, the total number of lines emanating through at the 2R sphere is the same as the R sphere. The field is inversely proportional to R squared, and the area of the sphere is proportional to R squared. So that means the product of the two is independent of R. Now for a sphere of a variable radius r, the magnitude E of the surface is:
(Equation 6-15)
The surface area of the sphere is:
(Equation 6-16)
This means that the product of the two is independent of r and depends only on the charge of q (since we are given everything else).
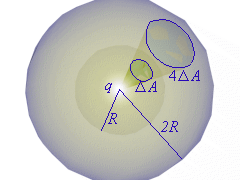Also, what is true of the entire sphere is true of any part of its surface.
Thus an area DA is outlined on the surface of a sphere, seen in the illustration to the right (click on the illustration for a VRML model of the Gaussian projection), of radius R and then projected onto the sphere of radius 2R (same example as before).
The area projected on the larger sphere is 4DA, which proves that the product EDA is independent of the radius of the sphere.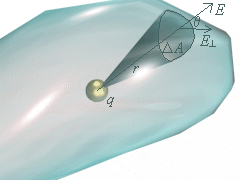
The reason for explaining this is for explanation of nonspherical surfaces.
Let's say we replace the second sphere with an irregular shape as seen in the illustation to the left (click on the illustration for a VRML model of the irregular shape).
Think about the small area element DA.
The area is larger than the area of a sphere if its distance from q were the same.
Now if a normal to the that surface makes an angle q with a radial line from q, two sides of the area projected on the spherical surface are foreshortened by a factor cos q.
Thus the quantity of EDA for the spherical surface is EDA cos q for the irregular surface.To sum it all up, divide the entire irregular surface into small pieces of DA. Calculate EDA cos q for each piece, and then add them together. So this is what we get, as long as the surface encloses the charge q:
(Equation 6-17)
Thus, a surface that encloses no charge (q = 0) produces the following result:
(Equation 6-18)
Now if you realized that the field varies from one point to another on the irregular surface, you are correct. This means that Equation 6-17 only applies when the limit of the area elements become really really small. This means that we must bring in integration, and in this case, the limit of the sum becomes a special surface integral of E cos q, written as follows:
(Equation 6-19)
You probably aren't used to the integral with the little circle on it, but it just tells you that it is taken over a closed surface enclosing the charge q (called a surface integral). Now we also know that E cos q is the component of E perpendicular to the surface each of the points so we will use a special notation (with the perpendicular sign) in replacing E cos q, which will make the equation look like this:
![surfaceintegral(E[perpendicular] dA) = q/(epsilon 0)](6-20.gif){kind=small}
(Equation 6-20)
This quantity is called the electric flux through the area dA. Electric flux is denoted by Y, and an element of flux of the small area dA is dY. Thus the following relationships are true (because we just defined them):
![d(Psi) = E[perpendicular]dA = E cos(theta) dA = E dot dA](6-21.gif){kind=small}
(Equation 6-21)
The total flux Y through a finite surface is the integral of dY, or:
(Equation 6-22)
Thus, we make the necessary substitutions to come to this brilliant conclusion:
(Equation 6-23)
Now what about multiple charges? We only talked about one charge, inside or outside, but only one charge. But remember that the total electric field E at a point on the surface is the vector sum of the field produced by any number of single charges within the surface. Which means that we could have one or one hundred charges within the surface, only the vector sum of these charges will be taken into effect and the vector sum acts as if it was just one charge. So to be thorough about the equation, it can be written as:
![Psi = summation(q)/(epsilon 0) = q[enc]/(epsilon 0)](6-24.gif){kind=small}
(Equation 6-24)
We called the sum of all the charges qenc to stand for all the enclosed charges.
Here is a quick list of rules that will help you calculate electric flux:
-
If E is at right angles to a surface of A at all possible points and E is constant at these points, then:
![E[perpendicular] = E = constant; therefore Psi = EA](6-25.gif)
(Equation 6-25) - If E is parallel to the surface at all points, the perpendicular component of E = 0 and so does the integral.
- If E = 0 at all points of a surface, the integral is zero.
- The surface you apply Gauss's Law to doesn't need to be a real physical surface. In most applications you use an imaginary surface that is actually empty space, embedded in a solid body, or partly in space and partly in body.
- In the integrals, E is always the total electric field at each point on the surface. In general the field is caused partly by changes within the volume and partly by charges outside, but even when there is no charge in the volume the field on the surface isn't necessarily zero. But in that case, however, EdA is always zero.
- In using Gauss's law to calculate fields, you need to know which surface to choose. The point or points at which the field is to be determined must lie on the surface and that the surface must have enough symmetry so that you can evaluate the integral. So if the problem has spherical symmetry, the easiest Gaussian surface (as it is called) to use would be a sphere.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar