FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Magnetic Fields of Currents |
 
|
Return to the Advanced Level Page.
You remember that a moving charge creates a B field and that currents are just moving charges. So, we will now discuss how these B fields as set up.
Magnetic Fields of a Current Element
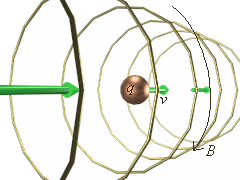The illustration at right shows the magnetic field set up by a moving charge q with a velocity v (click on the illustration for a VRML model of the moving charge).
Now, moving charges is basically current, right?
So, let's find the magnetic field set up by a current of i.
We will break up the current of this imaginary wire into current elements of i ds.
However, we should note that this current element is a vector quantity, so we need to take that into account by using an angle q.
So, we have the magnetic field of the current element to be:
(Equation 6-63)
m0 is a constant called the permeability constant and is equal to 4p x 10-7 T m/A. Sometimes, the value of m0/4p is just refered to as a constant k', which has the value of 10-7 T m/A. Anyway, continuing with our discussion, if you write Equation 6-63 in a more general term, using a vector cap over the r to indicate direction instead of using sin q, you get:
(Equation 6-64)
This is called the Biot and Savart Law (incidently, the names rhyme with "Leo and bazaar"; don't ask us why).
Magnetic Field of a Long Straight Conductor
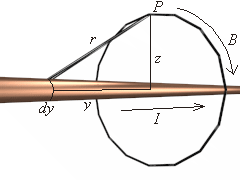We can use the Biot law to calculate the magnetic field of a long straight conductor carrying a current of I.
We will measure this field from an arbitrary point P outside the conductor as shown on the illustration at right (click on the illustration for a VRML model of the long straight conductor).
The length of the conductor will be 2L, and the midpoint is at the origin.The current element we will use to calculate the field is a distance r away from point P. The horizontal component of r is y; the vertical is z. So:
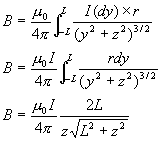
(Equation 6-65)
But since L is so much greater than z,it can be dropped out from inside the radical:
(Equation 6-66)
Notice that we replaced the z with an R. We did this so that you can think of the point as a distance of a radius around the wire.
Magnetic Field of a Circular Loop
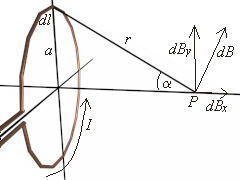As you notice in the illustration at right (click on the illustration for a VRML model of the circular loop), the coil is supplied current I through two straight sections.
You might wonder if perhaps that will affect the magnetic field in any way.
It turns out that it will not because the fields created will nullify one another.Let's do another derivation to illustrate this. Again, we will find the magnetic field and break it into components at point P shown in the illustration:
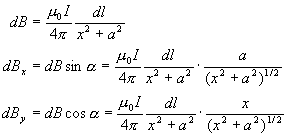
(Equation 6-67)
But because of symmetry, you can tell that the y-component is cancelled out by the opposite sides of the ring. So only the x-component is matters, so we integrate it and get:
(Equation 6-68)
And look what familiar equation you get when point P is at the center of the loop (x = 0):
![B[x] = (mu 0)I/2a](6-69.gif){kind=small}
(Equation 6-69)
Force Between Parallel Conductors
If you had two long straight parallel conductors each with currents (I and I') in the same direction, the magnetic fields generated by each of the currents will interact and cause a force between them. Since the magnetic field of the first conductor is:
(Equation 6-70)
the force on the other conductor must be:
(Equation 6-71)
To find the direction of the force, use the right hand rule, and you will find the the wires attract each other. If the currents in the two wires are going in opposite directions, then the wires will repel (notice that this is one exception to the usual, "opposites attract").
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar