FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Kirchhoff's Loop Laws |
 
|
Return to the Advanced Level Page.
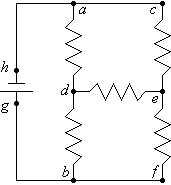Since not all circuits can be reduced to simple series-parallel combinations, we need new rules to work with when we have resistence networks of cross connections such as the illustration at right.
In such a circuit, a branch point is a point where three or more conductors are joined.
A loop is any closed conducting path.
In the diagram, a, d, e, and b are branch points but c and f are not.
aceda, defbd, and hadefbgh are examples of loops.
Now, concerning networked cross connections, there are only two relatively simple rules known as Kirchhoff's rules (developed by Gustav Robert Kirchhoff (1824-1887)).-
Point Rule: The algebraic sum of the currents toward any branch point is zero.
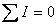
(Equation 6-57)
-
Loop Rule: The algebraic sum of the potential differences in any lopp, including those associated with EMFs and those of resistive elements, must equal zero.
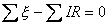
(Equation 6-58)
- Choose any closed loop in the network and designate a direction to traverse the loop when you apply the loop rule (If you have a diagram, draw it on the diagram).
- Go around the loop in that direction, adding EMF's and potential differences. An EMF is positive if you go from (-) to (+) (which is in the direction of the field E in the source) and negative when you go from (+) to (-). A -IR term is counted negative if the resistor is traversed in the same direction as the assumed current, positive if backwards.
- Equate the sum of found in the previous step to zero.
- If you need to, choose another loop to obtain a different relationship. The number of loop equations you have will be one less than the number of loops you have. You will be setting up a system of equations in order to find the current in each loop.
- The last equation should be a branch equation, where I1 + I2 = I3 (substitute the currents for whichever branch you choose).
- Solve the systems of equations. If one of the currents you solve is negative, it simply means that the current goes in the direction opposite the way you assumed. Remember, switch the current for only that current.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar