FizziCalc
Intermediate
Advanced
Cool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Rotational Mechanics |
|
Return to the Advanced Level Page.
Until now we only played around with the translational motion of particles, be it balls, rocks, spaceships, or falling water. Now we will do something a little different. Now whenever you throw, let's say a ball, you know that not only does it fly through the air but chances are that it will spin in some way. That spin, or rotation, is what we will be discussing now, the kinematics and mechanics of rotational motion.
Angular Displacement and Velocity
 When that ball you throw is spinning, it spins with a certain velocity (independent of the velocity of the ball itself as it flies through the air) that is called angular velocity.
Like our usual translational velocity, angular velocity is basically the change in angular displacement over the change in time.
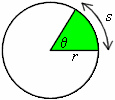
In the illustration on the right we can see that linear displacement (across the circumference of the circle labeled s) is related to the radius of the circle and angular displacement q.
In fact, the linear displacement is merely qr.
Please note that q is in units of radians, not degrees (1 radian = 180/p degrees).
When that ball you throw is spinning, it spins with a certain velocity (independent of the velocity of the ball itself as it flies through the air) that is called angular velocity.
Like our usual translational velocity, angular velocity is basically the change in angular displacement over the change in time.
In the illustration on the right we can see that linear displacement (across the circumference of the circle labeled s) is related to the radius of the circle and angular displacement q.
In fact, the linear displacement is merely qr.
Please note that q is in units of radians, not degrees (1 radian = 180/p degrees).Angular velocity is the change in angular displacement over a change in time. Thus angular velocity (w) is defined as follows:
(Equation 5-1)
You may notice we use the greek letter w instead of plain old v. This is to distinguish between velocity and angular velocity.
Angular Acceleration
Similar to translational kinematics, angular acceleration (a) is merely the change in angular velocity over the change in time:(Equation 5-2)
Please note that the linear acceleration used here is the acceleration of a point on the circle parallel, or tangent, to its surface (thus, it is sometimes called tangental acceleration). This is not to be confused with centripetal acceleration, which is the acceleration towards the center of the circle.
To recap:
![s = r(theta); v = r(omega); a[parallel] = r(alpha); a[perpendicular] = r(omega^2)](5-3.gif)
(Equation 5-3)
The equation for centripetal equation in terms of angular quantities is the last line written above.
Kinematics Equations, Angular Style
You know what? You can do the exact same derivations we did with translational kinematics to find rotational kinematics equations if we are considering a case with constant angular acceleration. Basically, what comes out is essentially the same equations but with different variables: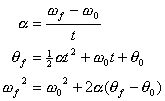
(Equation 5-4)