Beginner Intermediate Advanced Cool Topics Reference Search

Games and Fun Stuff Feedback Meeting Forum
Main Page
FizziCalc
Topics
Beginner
Intermediate
Advanced
- Brief Calculus Overview
- Vector Products
- Kinematics with Calculus
- Mechanics with Calculus
- Rotational Mechanics
- - Rotational Inertia
- - Torque
- - Angular Momentum
- Electricity and Magnetism
- - Electric Fields
- - Gauss's Law
- - - Applications
- - Electric Potential
- - Capacitors
- - Kirchhoff's Loop Laws
- - Magnetic Fields
- - - Fields of Currents
- - - Ampere's Law
- - Induced EMF
- - Inductance
Cool Topics
Reference
Features
Customize
Search
Games and Fun Stuff
Meeting Forum
Physics Links

Kinematics with Calculus

 Back Next
Return to the Fizzics Fizzle Main Page.
Return to the Advanced Level Page.
If you have taken Physics in the past or have read through our intermediate section, you will already have a very thorough understanding of kinematics and many of its equations. However, it is useful to derive these equations as they were originally derived by the Newton with the use of calculus. This is important because it will also solidify the fundamental calculus you learned earlier and it will also be good practice for when you derive other equations in other topics in physics. The earlier you have a familiarity with calculus and its use in physics, the better.

You know that velocity is the change in displacement over the change in time, and acceleration is the change in velocity over the change in time.
Now express velocity as "the change in displacement over the change in time" as a derivative and you get:
v = ds/dt
(Equation 3-1)

That shows that velocity is the derivative of displacement, and in likewise, the integral of velocity is displacement. Now apply this to acceleration and you get:
a = dv/dt
(Equation 3-2)

The derivative of velocity is the acceleration.

Now one of the cases of motion that we dealt with heavily in the intermediate section is when acceleration is constant. We shall start with constant acceleration and move our way backwards to displacement. First, let's find the velocity at any point in terms of the acceleration:
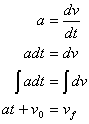
a = dv/dt; a dt = dv; integral(a dt) = integral(dv); at + v0 = vf
(Equation 3-3)

Now let's go over what we did:
  1. Acceleration is the derivative of velocity, as we said before.
  2. Multiply both sides by dt.
  3. Take the indefinite integral of both sides.
  4. The indefinite integral of the left side leaves a constant, which is the initial velocity (v0). The indefinite integral of the right side gives us the final velocity (vf).
Now, the final velocity is based on the change in displacement over the change in time. Thus, we can similarly repeat what we did before to get the displacement:
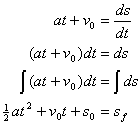
at + v0 = ds/dt; (at + v0)dt = ds; integral((at + v0)dt) = integral(ds); 0.5at^2 + v0t + s0 = sf
(Equation 3-4)

Doesn't that equation look almost like the one that was used in the intermediate section?
Back Next
Created by TQ Team 16600: Clyde Law, Chetan Taralekar, Jim Wang
 E-mail us!
Team Coaches: Melanie Krieger, Chhaya Taralekar