FizziCalc
Intermediate
Advanced
Brief Calculus OverviewVector ProductsKinematics with CalculusMechanics with CalculusRotational MechanicsRotational InertiaTorqueAngular MomentumElectricity and MagnetismElectric FieldsGauss's LawApplicationsElectric PotentialCapacitorsKirchhoff's Loop LawsMagnetic FieldsFields of CurrentsAmpere's LawInduced EMFInductanceCool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Vector Products |
 
|
Return to the Advanced Level Page.
Many times in physics we talk about the products of vectors, but with something that has a direction and a magnitude (two parts), you probably don't know how to multiply them unless you have had exposure to dot and cross Products. Adding vectors was different that adding normal numbers, and you will find multiplying vectors is really different from multiplying numbers. Now before you start, there are two different kinds of vector products that are used:
- Scalar Product: yields a scalar as the answer, not a vector; commonly called the dot product.
- Vector Product: yields a vector with a direction perpendicular to the plane formed by the two vectors being multiplied; commonly called the cross product
Dot Product
The scalar product of two vectors, we'll call them A and B, separated by an angle of q, is defined as:Thus, when q is an acute angle, the dot product is positive; when q is obtuse, the dot product is negative; when q is a right angle, the dot product is zero. This is because of the nature of the cosine function, cosine is positive from 0° to 90°, zero at 90°, and negative from 90° to 180°.
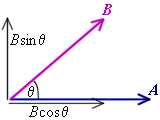Now, in the illustration to the right, Vector B can be split into its components.
The component parallel to A is B cos q.
That means that A · B (read as "A dot B") is equal to the parallel component of B multiplied by the magnitude of A.
The reverse is true as well.
The component of A parallel to B multplied by B will yield the same result.Cross Product
The magnitude of the vector product of two vectors, again A and B, separated by an angle of q is defined as:The equation has a sine function within it, just as dot product had a cosine, so that means if the angle is 0°, then you get a magnitude 0. Thus, parallel vectors have a cross product of 0 just as dot products of perpendicular vectors are 0.
The cross product is a vector quantity with a direction perpendicular to the plane of the two vectors and a magnitude given by the above equation. But as you know from elementary geometry, there are two directions perpendicular to a given plane (up or down?) and to distinguish in which direction the vector is going, there is a simple hand rule.
Imagine rolling vector A around the perpendicular vector (direction currently unknown) towards B. Now curl the fingers of your right hand so they trace the imaginary path of vector A. Stick your thumb out and the direction of the vector is the same direction your thumb is facing. That is known as the right hand rule (If you are wondering why this is similar to the right hand rules in electricity and magnetism, it is electricity and magnetism require cross products).
An alternate rule to use, if you can't tell your right hand from the left, is the screw rule. If you point a screw and turn it in the same rotational direction as the imaginary path, the direction the screw moves is the direction of the vector (clockwise is inward; counterclockwise is outward).
However, unlike the dot product, you will not have the same answer if you roll B into A. This equation is not commutative. If you do B × A, then your answer will be the negative of the magnitude of A × B (in other words, the vector product faces the opposite direction).
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar