FizziCalc
Intermediate
Advanced
Cool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Circular Motion |
|
Return to the Intermediate Level Page.
Newton's first law states that an object in motion remains in motion at constant velocity unless acted upon by an outside force. If the force is applied perpendicular to the direction of motion, only the direction of velocity will change. If a force constantly acts perpendicular to a moving object, the object will move in a circular path at constant speed. This is called uniform circular motion.
The force that keeps an object moving in a circular path is called the centripetal force. You may have heard about centrifigal force before. Many people confuse centrifugal and centripetal forces. However, there is no such thing as centrifugal force. We will explain this confusion.
Have you ever been in one of those amusement park rides where you are spun around and around? Did you feel as if you were pressed against the outside of the circle? Many people call this the centrifugal force. However, a centrifugal force does not exist. The only force acting is the centripetal force, which is pulling you inward toward the center of the circle. The reason you feel a centrifugal force is because the car that you are in is pulled toward the center of the circle, but due to Newton's first law, you want to keep going forward.
If you are still a bit confused by this explanation, here's a simpler one that doesn't involve circles. If you are in a car that's speeding up, you get pushed back in your seat, right? However, is there an actual force that is pushing you back? No, the only force is the force that is pushing the car forward. You feel a force pushing you back because you tend to remain in the same position while the car moves forward. This is similar to the centrifugal feeling.
 Now that we have that cleared up, let's start going into the details of centripetal force.
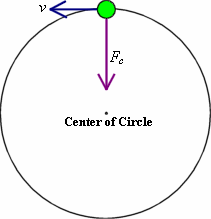
An object will move around a point in a circle if there is a centripetal force that is constantly directed towards the middle of the circle.
Also notice how the velocity vector is always pointed tangent to the circle.
If you suddenly remove the centripetal force from an object that is moving in a circle, it will not fly outward from the center, but rather tangent to the circle.
To calculate the centripetal force (Fc) needed to move an object at constant velocity in a circle:
Now that we have that cleared up, let's start going into the details of centripetal force.
An object will move around a point in a circle if there is a centripetal force that is constantly directed towards the middle of the circle.
Also notice how the velocity vector is always pointed tangent to the circle.
If you suddenly remove the centripetal force from an object that is moving in a circle, it will not fly outward from the center, but rather tangent to the circle.
To calculate the centripetal force (Fc) needed to move an object at constant velocity in a circle:
(Equation 1-19)
If you divide both sides by m, you can find the centripetal acceleration (ac):
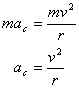
(Equation 1-20)
You should note that even though the object is moving at constant velocity, it is not in equilibrium because it is changing directions.
Check out the Orbit Explorer in our games and fun stuff section to see how a body orbits another body.