FizziCalc
Intermediate
MechanicsKinematicsForce and EquilibriumEnergy and WorkMomentumGravitationCircular MotionSimple Harmonic MotionElectricity and MagnetismStatic ElectricitySimple CircuitsMagnetismAdvanced
Cool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Kinematics |
 
|
Return to the Intermediate Level Page.
Kinematics is a mathematical description of motion without regard to the forces that produce it. So what does that mean? Let's say you throw a ball across the park. Kinematics will describe how the ball will traverse through the air after it leaves your hand. It does not deal much with how you threw the ball though.
Before we begin with how you can describe the ball's behavior, we have to go through the definitions of displacement, velocity, and acceleration. These three quantities are known as vector quantities (if you are a bit unsure about how to use vectors, check out Beginner: Basic Kinematics). Vectors are described using both magnitude and direction.
Displacement will tell you how far and in which direction the ball travels. It is usually denoted with the variable s.
Velocity will tell you how the displacement changes over a certain period of time. It is usually denoted with the variable v. Since the average velocity is the change in displacement over the change in time, you can write:
(Equation 1-1)
The line above the v means that it is the average velocity.
Acceleration will tell you how the velocity changes over a certain period of time. It is usually denoted with the variable a. Since the average acceleration is the change in the velocity over the change in time, you can write:
(Equation 1-2)
In straight line motion, you can use graphs to show the correlation between the three quantities.
Constant Velocity Graphs:
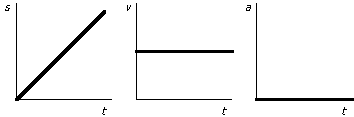
Constant Acceleration Graphs:
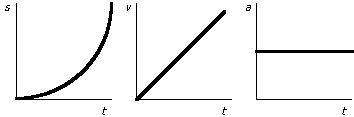
Let's take a look at what these graphs mean. In the constant velocity graph, constant velocity means that there is no acceleration, thus the acceleration is 0 throughout on the right graph. Velocity is constant as seen in the middle graph. On the left graph, you see that displacement is increasing as time continues. Also notice how displacement is increasing linearly (uniformly) because of a constant velocity.
In the case of constant acceleration, you see that velocity is increasing linearly in the middle graph because it is accelerating uniformly. Because of this, the displacement is increasing higher and higher, quicker and quicker, as time progresses.
If you look into the graphs a bit further, you may notice that the slope of the displacement graph at a certain time is the same as its velocity at that certain time (called instantaneous velocity). Likewise, the slope of a velocity graph at a certain time is the instantaneous acceleration. Instantaneous velocity/acceleration is different from average velocity/acceleration since it measures the slope at that time, whereas average measures the slope from one time to another.
This next thing is harder to tell from the graphs, but you may tell that the area of the velocity graph up to a certain time is the same as the change in time up to that point. Likewise, the area of the acceleration graph is the change in velocity up to that point.
Motion in a Plane
So what about that ball? Can we tell where it is going to land? Using kinematics, we can.Let's say we threw it initially with a velocity of 20 m/s at an angle of 30° into the air. When the ball leaves our hands, what happens? For the moment, let's neglect air friction since it is unpredictable and irrelevant in our discussion. Well, the ball is moving both horizontally and vertically, right? The force of gravity is also acting on the ball in the vertical direction, right?
Okay, let's put this together in the form of some equations. Since no forces are acting on the ball in the horizontal direction, we can say that it is moving at contant velocity horizontally because of Newton's First Law of Motion. Thus, we can say that its horizontal displacement (sx) is merely equal to its horizontal velocity (vx) times the change in time.
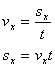
(Equation 1-3)
The vertical direction is a bit different since it involves constant acceleration. This is the equation that is used:
(Equation 1-4)
What does that mean? Well, the vertical displacement (sy) is equal to one half the acceleration times the change in time squared plus the initial veritical velocity (vy0) times the change in time. The part with the acceleration in it is used to account for the fact that its vertical velocity is changing because of gravity.
So, let's finish the problem that we have. First we should figure out our initial horizontal and vertical velocities:
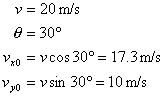
(Equation 1-5)
Substitute these values into the vertical displacement equation to find the time it takes for the ball to go up and fall back down. Since it goes up and falls back down, its vertical displacement is 0. Also, because gravity acts downward, we have to use a negative 9.8 m/s2 for the acceleration. Once we have the time, we can substitute it into the equation for the horizontal displacement.
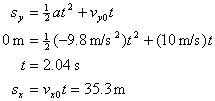
(Equation 1-6)
And you are done! You threw the ball about 35.3 m. Wow, you have a pretty good arm.
This is just one example of the various kinematics problems you can solve. These are some other equations that you can use to solve problems involving constant acceleration:
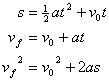
(Equation 1-7)
The first one is just the one that we used in the previous example. The second one states that the final velocity (vf) is equal to the initial velocity (v0) plus the quantity of acceleration times the change in time. The third one allows you to find the final velocity using your initial velocity, acceleration, and displacement.
Check out the Projectile Motion in our games and fun stuff section to apply your kinematics knowledge to shoot a basketball into a hoop.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar