FizziCalc
Intermediate
MechanicsKinematicsForce and EquilibriumEnergy and WorkMomentumGravitationCircular MotionSimple Harmonic MotionElectricity and MagnetismStatic ElectricitySimple CircuitsMagnetismAdvanced
Cool Topics
Reference
Search
Games and Fun Stuff
Meeting Forum
Physics Links
Gravitation |
 
|
Return to the Intermediate Level Page.
Issac Newton devised a universal law of gravitation that stated all objects exert a gravitational force of attraction on each other even when separated by large distances. The force of gravity between two masses (m1 and m2) separated by a distance (r) is:
(Equation 1-16)
G is a constant that equals roughly 6.67 x 10-11 N m2/kg2.
We can actually use this to derive the value of g (acceleration at the surface of the earth due to gravity). We will let m1 equal the mass of the earth, which is roughly 6.0 x 1024 kg. Also, m2 can be any arbitary mass; it will be cancelled out later as you will see. And finally r will be the radius of the earth (roughly 6.4 x 106) since we want the acceleration at the surface. Now let's begin:
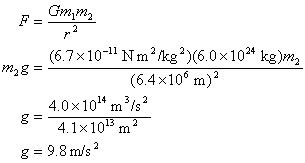
(Equation 1-17)
...and we get our good old 9.8 m/s2.
Kepler's Laws
Johannes Kepler was a 16th century astronomer who studied the motion of the planets. Through years of analyzing data, he came up with three laws that govern the motion of the planets around the sun. He arrived at them trial-and-error, but Newton's laws of motion and gravitation would later explain why they were true.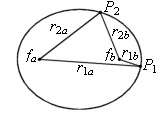
Kepler's first law states that the orbits of all the planets are not circles but ellipses.
An ellipse is a closed curve in which the sum of the distances from any point on the curve to two fixed points called the foci is constant.
The illustration at right is an ellipse with two foci, fa and fb.
The sum of the distance between the foci and point P1 (r1a + r1b) is equal to the distance between the foci and point P2 (r2a + r2b), or between the foci and any other point on the ellipse for that matter.An ellipse looks like a flattened circle. The greater the distance between the two foci, the greater the eccentricity of the ellipse. If the foci are located at the same point, the ellipse becomes a perfect circle. Planets orbiting the sun are traveling in slightly elliptical orbits but they seem circular because the distance between the foci is small. In an orbit, the sun is located at one of the foci.
Kepler's second law states that a planet orbiting the sun always sweeps out the same area in an equal amount of time.
In the illustration at right, the area labeled 1 is equal to the area labeled 2.
This is because when the planet is closer to the sun, it orbits faster, sweeping a greater arc in a certain amount of time.
When the planet is farther from the sun, it orbits slower, sweeping a smaller arc in the same amount of time.
This accounts for the fact that at any time, the planet will sweep the same exact area.Kepler's third law is a relationship between the mean radius of a planet's orbit (R) and it's period of revolution (T):
(Equation 1-18)
K is a constant that is the same value for anything orbiting the sun. This constant has a value of roughly 2.5 m3/day2. We can use this relationship to find the mean orbit radius of every planet if we know the periods.
Clyde Law, Chetan Taralekar, Jim WangMelanie Krieger, Chhaya Taralekar